Editorial: Codeforces 1666L: Labyrinth

Problem Link: codeforces.com/problemset/problem/1666/L

This Problem has various ways to solve but today I am going to talk about the ways which help you understand the important technique which will help you in various graph problems.

In this problem, we need to return two paths which starts from s and ends at t and they have no common nodes instead of s and t.

The naive way to solve this problem is to take each node (apart from s) as t and then check whether there is a path that will not coincide with each other. But this operation is very costly since N is 2e5, It will give TLE.

Now we need to optimize our approach. Let's say if we are able to determine t, can we find the path? the answer is hell yes.

Our main idea is to use the multiple values in the visited array, mainly 0,1,2 where 0 means nodes is not visited yet,1 means node is visited but not explored yet, and 2 means node is visited and explored.

Now the question arises, What is the meaning of node is explored? It means it has no children to be explored now. Lets me explain with this example Suppose there is graph 1->2->3,1->4 and s = 1, we will start the dfs from s, vis[s] = 1,then we will go to 2, vis[2] = 1, then we will go to 3, vis[3] = 1, but after 3 there are no nodes to go, so we will mark vis[3] = 2, now it will go back to 2 , we see no nodes left for 2 too, vis[2] = 2, but then we go to node 1 then It will go to node 4,vis[4] = 1, now no nodes left for vis[4] = 2, at the end vis[1] = 2 since no nodes are left to be explored.

While during dfs, if we encounter a node that is explored already, then the node can maybe be our answer. Now how to determine the correct node, for that we need to check out the path.

It is a very obvious thing that if the path starts from s, the second node will be the child of the s. So we will use the from the array which will determine from where the path is coming.

Consider this graph

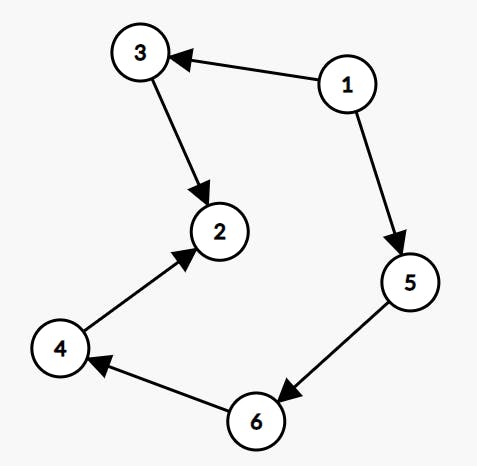
we will consider the from array, for node 3 and 5 , from[3] = 3 and from[5] = 5. For node 5, from[6] = 5, then dfs from 6, it will go to 4 and from[4] = 5, and so on. so it makes sense if we want the paths not to coincide then the from[u] != from[v] where u and v are nodes and vis[u] = 2.

These conditions will determine the node t correctly and we will have a parent array that will store the parent of node so that we can find the path.

Here is the implementation of this problem

int n,m,s;
const int N = 2e5 + 5;
vector<int> adj[N];
vector<int> from(N),vis(N),par(N);
int node1,node2,ans = 0;


void dfs(int node,int parent){
    if(ans){
        return;
    }
    vis[node] = 1;
    from[node] = parent;
    for(auto child : adj[node]){
        if(vis[child] == 0){
            par[child] = node;
            if(!parent){
                dfs(child,child);
            }else {
                dfs(child,parent);
            }
        }else if(vis[child] == 2){
            if(from[child] != from[node]){
                node1 = child;
                node2 = node;
                ans = 1;
                return;
            }else {
                continue;
            }
        }else {
            continue;
        }
    }
    vis[node] = 2;
}


void solve() {

    cin >> n >> m >> s;
    for(int i  = 0;i < m;i ++){
        int a,b;
        cin >> a >> b;
        adj[a].push_back(b);
    }
    dfs(s,0);
    if(!ans){
        cout << "Impossible\n";
        return;
    }
    int temp = node1;
    vector<int> ans1,ans2;
    while(node1 != s){
        ans1.push_back(node1);
        node1 = par[node1];
    }
    while(node2 != s){
        ans2.push_back(node2);
        node2 = par[node2];
    }
    ans2.push_back(s),ans1.push_back(s);
    reverse(all(ans1));
    reverse(all(ans2));
    ans2.push_back(temp);
    cout << "Possible\n";
    cout << sz(ans1) << nline;for(auto i : ans1) cout << i << ' ';
    cout << nline;
    cout << sz(ans2) << nline;for(auto i : ans2) cout << i << ' ';
    cout << nline;
}

I hope I am able to explain my approach properly. If you have some doubts regarding this approach or you have a new approach to solve this problem, do let me know in the comment section.

Thankyou!